Have you ever wondered why certain roofs seem to float effortlessly while using minimal material? Exploring the Geometry of the Hyperbolic Paraboloid unlocks that mystery. This saddle-shaped, doubly ruled surface is not only a marvel in mathematics but also a structural superstar in architecture and design. In fact, thin-shell concrete structures using this geometry can span tens of meters with a thickness of just a few centimeters, a feat pioneered by engineers like Félix Candela. According to ArchDaily, Candela’s Los Manantiales restaurant demonstrates the combination of elegance and structural efficiency that this form makes possible.
Unlock More Insights
Instant Answer
The hyperbolic paraboloid is a saddle-shaped surface with negative curvature that distributes load efficiently, allowing architects and engineers to build complex curves using straight elements.
This shape combines aesthetic appeal with material efficiency and can be applied in everything from paper models to massive concrete shells.
What Exactly Is a Hyperbolic Paraboloid?
A hyperbolic paraboloid is a surface that curves upward in one direction and downward in another, giving it the iconic saddle shape.
Exploring the Geometry of the Hyperbolic Paraboloid reveals that it is a doubly ruled surface, meaning two sets of straight lines lie on the surface. Architects and engineers love it because these straight lines allow easy construction of complex curves.
Impressive phenomenon isn’t it? But its more attractive with visuals try watching the given video covering the same topic in detail:-
“Explore Geometry: Hyperbolic Paraboloid“
Why does it look like a Saddle?

The Saddle Point and Negative Curvature
The saddle point occurs where curvature changes direction. Gaussian curvature is negative at every point, which is why the surface bends like a Pringles chip.
Double Ruling: Two Families of Straight Lines
Two distinct straight-line families cover the surface entirely. Following these lines allows builders to construct curved roofs using simple, straight beams.
How Does Its Saddle Geometry Actually Work?
Exploring the Geometry of the Hyperbolic Paraboloid shows that Gaussian curvature is negative everywhere, creating a natural saddle effect. This means every point acts like a mini structural stabilizer. Principal curvatures, k₁ and k₂, are opposite in direction, allowing efficient distribution of loads in thin-shell structures.
Understanding Gaussian Curvature Negative
Negative curvature ensures that the surface resists bending in all directions while maintaining elegance.
Principal vs Mean Curvature in Hypar
The principal curvatures dictate stiffness along each axis, while mean curvature remains zero in ideal minimal surfaces.
Visualizing Asymptotic Directions
Lines along which curvature is zero help guide straight beam placement during construction.
Key Intake: Negative curvature stabilizes the hypar (Hyperbolic Paraboloid) surface.
Why Do Architects Keep Choosing This Shape?
Architects have long relied on Exploring the Geometry of the Hyperbolic Paraboloid to achieve dramatic, lightweight, and elegant roofs. Structures like the TWA Flight Center curves and St. Mary’s Cathedral hypar showcase minimal material use with maximum span. Thin-shell concrete allows spans of over 30 meters with shells as thin as 40 mm, proving both aesthetic and structural appeal.
Structural Benefits of Saddle Geometry
Saddle-shaped surfaces naturally distribute stress and reduce bending moments.
Iconic Examples and Material Efficiency
Candela’s Los Manantiales, Philips Pavilion, and Saddledome roof demonstrate both the elegance and efficiency of hypar shells.
Key Intake: Hypar geometry combines beauty, strength, and minimal material usage.
How Can Straight Beams Build Such Complex Curves?
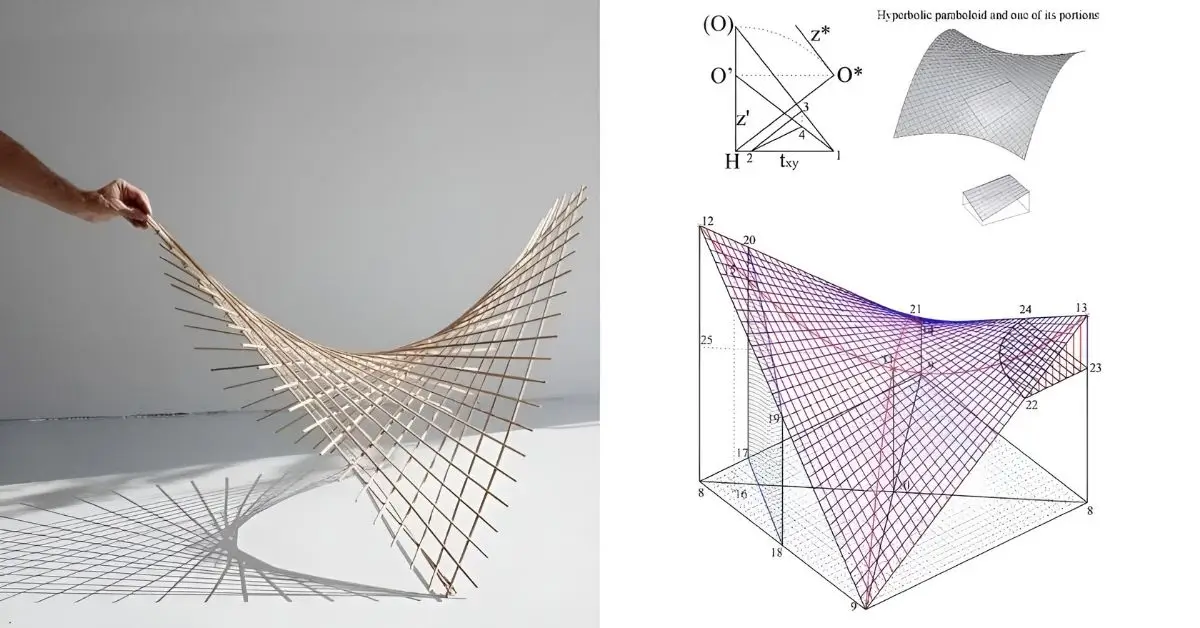
Exploring the Geometry of the Hyperbolic Paraboloid shows that its doubly ruled surface allows straight beams to follow the natural lines of the surface. This eliminates the need for curved formwork, saving cost and complexity.
Straight Beam Construction Explained
By arranging beams along the ruling lines, builders can achieve the saddle shape without bending.
Timber, Steel, Bamboo Methods
Modern constructions use timber, steel, bamboo, and even plywood to form hypar roofs efficiently.
Modern Parametric Formwork
Parametric modeling can optimize panel layouts, even for complex free-form structures.
Key Intake: Straight beams naturally form curves along the hypar’s geometry.
What Makes the Cornell Sculpture and Candela’s Shells Iconic?
Candela’s shells and Don Greenburg’s Cornell sculpture show the power of Exploring the Geometry of the Hyperbolic Paraboloid in real-world applications. These structures achieve vast spans using extremely thin shells, leveraging geometry over mass.
Los Manantiales Case Study
Shells only 40 mm thick span over 30 meters, proving minimal material use is possible.
Cornell Sculpture Analysis
Students built the 1966 Cornell hypar sculpture with straight plywood, demonstrating hands-on feasibility.
Key Intake: Real-world examples confirm the strength and elegance of the hypar.
How Did Origami Inspire NASA’s Design Breakthroughs?
Folding techniques from Exploring the Geometry of the Hyperbolic Paraboloid inspired deployable structures, including the James Webb Space Telescope sunshield. Concentric squares with alternating mountain and valley folds scale up perfectly from paper to high-tech engineering applications.
- Concentric Squares Folding Technique: Crease patterns fold into a saddle shape.
- Mountain and Valley Folds Explained: Alternating folds create the three-dimensional hypar form.
- From Paper to Space: JWST Sunshade: Origami principles allow efficient deployment of massive, precise surfaces.
Key Intake: Paper folds scale to deployable engineering solutions.
Can Hypar Forms Be Sustainable Too?

Exploring the Geometry of the Hyperbolic Paraboloid reduces material use and carbon footprint. Hypar roofs cut embodied carbon by 30–40% compared to conventional steel or concrete roofs. Bamboo, timber, and mass timber structures further enhance sustainability without sacrificing strength.
- Embodied Carbon Savings: Material efficiency is the primary sustainability benefit.
- Sustainable Material Options: Bamboo, timber, and recycled concrete are excellent options.
Key Intake: Geometry drives material efficiency and greener construction.
How Do Designers Model These Surfaces in Rhino or Grasshopper?
Parametric software allows designers to explore Exploring the Geometry of the Hyperbolic Paraboloid digitally before construction. Rhino with Grasshopper generates the form, Karamba3D or SAP2000 perform structural analysis, and AutoCAD/Revit produces fabrication drawings.
- Parametric Modeling Hypar: Surface parametrization allows dynamic adjustments.
- Mesh Discretization & Surface Parametrization: Panelization strategies simplify fabrication.
- Exporting for Analysis and Fabrication: FEA ensures load paths and stability are verified.
Key Intake: Digital tools make complex hypars easy to design and validate.
Can You Build or Fold a Hyperbolic Paraboloid Yourself?
DIY approaches allow hands-on learning. Small-scale plywood roofs, string grids, or paper models make Exploring the Geometry of the Hyperbolic Paraboloid tangible for students, makers, and designers.
- Paper Origami Hypar Model: Fold grids with mountain and valley creases for classroom demos.
- DIY Plywood Roof Formwork: Straight strips can create miniature shell roofs.
- Scaling Lessons to Digital/Parametric Models: Hands-on experience informs digital parametric design.
Key Intake: Anyone can explore hypar geometry hands-on.
Conclusion
Exploring the Geometry of the Hyperbolic Paraboloid reveals more than just a mathematical curiosity, it’s a blueprint for elegance, efficiency, and innovation. From Pringles-shaped folds in classrooms to Candela’s soaring concrete shells, this saddle-shaped form blends beauty with structural genius. Whether in origami, residential roofs, or parametric digital models, mastering its curves unlocks creativity while respecting materials and physics. In short, understanding the hyperbolic paraboloid empowers designers, engineers, and makers to turn complex geometry into practical, breathtaking reality.
FAQ’s
Q1: Is a hyperbolic paraboloid the same as a minimal surface?
Only if parameters a and b are equal; otherwise, it’s a constant mean curvature surface.
Q2: What is the simplest way to explain a hyperbolic paraboloid to a student?
It’s the shape of a Pringles chip made from weaving straight strips.
Q3: Can hyperbolic paraboloids be used for residential construction?
Yes, they are excellent for dramatic, efficient roofs but need expert engineering.
Q4: What materials, besides concrete, work well for building hypars?
Timber, plywood, steel bars, bamboo, and fabric membranes all work.
Q5: Why did Félix Candela favor the hyperbolic paraboloid shape
He valued efficiency, buildability, and its striking aesthetic potential.
Author Bio
Dr. Keiran Voss is a Structural Geometrist & Designer, with over 12 years of experience, Dr. Voss specializes in efficient, buildable, and visually stunning thin-shell structures and parametric forms.